Plane-Wave Analysis of Solar Acoustic-Gravity Waves: a (Slightly) New Approach

Richard S. Bogart & Luiz A. D. Sá,

Center for Space Science & Astrophysics, Stanford Univerity

Thomas L. Duvall, Jr.

NASA Goddard Space Flight Center

Laboratory for Astronomy and Solar Physics

Deborah Haber & Juri Toomre

Joint Institute for Laboratory Astrophysics, University of Colorado

Frank Hill

National Solar Observatory, National Optical Astronomy Observatories

Table of contents

Introduction
Analysis Technique
Discussion
Plans for SOI Analysis
References

Abstract

Plane-wave decomposition of acoustic-gravity wave effects observed in the photosphere provides a computationally efficient technique for probing the structure of the upper convective zone and boundary, where the flat-sun approximation is reasonably accurate. We describe the technique to be used for systematic plane-wave analysis of MDI data as part of the SOI data analysis pipeline, and the SOI analysis plan. We present estimates of sensitivity and discuss the effects of using different planar mappings. The technique is compared with previous approaches to the 3-dimensional plane-wave problem.

Introduction

Although the Sun is not flat, it is comparatively large. At least at some scale, analysis of local motions in the upper part of the convective envelope can be performed in plane geometry. In particular, the Sun's internal acoustic-gravity waves observed in the photosphere can be analyzed as if they were plane waves, even though they are in fact constrained to the eigenmode solutions of the wave equation in a nearly spherical cavity. Analysis of the 5-minute oscillations did originally proceed (largely for observational reasons) as a two-dimensional plane-wave problem, before and for some time after the recognition of these oscillations as global modes. In this approach, only waves propagating in one direction along the solar surface (parallel to an observing slit) were detected. With the advent of imaging Doppler detectors, helioseismology has become almost exclusively spherical.

It has been demonstrated that a full three-dimensional plane-wave analysis of solar oscillations can be readily performed and the results inverted to yield at least plausible inferences about the dynamics of the upper convective envelope (Hill, 1988).

In a plane geometry, the dynamical equations governing acoustic-gravity waves can be written very simply. It is quite straightforward to show that a motion relative to the observer of the field in which the waves propagate results in an apparent frequency shift proportional to the dot product of the velocity vector and the horizontal wave-number vector v(x,y,z) · k(x,y,z), suitably averaged in depth z for each eigenmode. Variations in sound speed produce frequency shifts proportional to the square of the wave number.

Analysis Technique

The first problem to be overcome in plane-wave analysis of solar waves is the mapping of the observed surface to a plane. It is assumed that the relative positions of any two points fixed on the Sun (in whatever heliographic coordinate system we choose) remain the same. The mapping can be done trivially by not ``mapping'' at all, i.e. by using the nearly orthographic projection of a spherical surface onto a plane from a point almost infinitely far away. It is pretty clear however that this is not the best mapping to use, or even a particularly good one, since (a) the scale changes depending on the location of the observed region with respect to disc center, and (b) the outer layers of the Sun are known to rotate at roughly 2 km/sec and this will introduce a basic frequency shift for all modes. The mapping that has found favor so far is Postel's azimuthal equidistant projection, in which the geodesics passing through a selected point are mapped as straight lines with equal intervals representing equal distances on the surface. (For a discussion of this and other common map projections, see Richardus & Adler 1972.) We have experimented with about a dozen standard cartographic mappings, comparing the distortions in the shapes of the power spectra as larger areas of the sphere are mapped. We find that the projection that minimizes distortions in the region of interest is Lambert's azimuthal equivalent (equal area) projection, but the differences among most of the reasonable choices, including Postel's, are slight. For purposes of comparison with other approaches, we have adopted Postel's projection for this work.

The mapping from heliographic coordinates implicitly involves tracking of the solar surface, at least to the extent that the heliographic coordinate system reflects the mean motion of the surface. Since the photosphere rotates differentially, the question of which coordinates to use is not trivial. There are three basic choices: to assume rigid body rotation (using the Carrington coordinates for example); to assume uniform rotation of the field of interest, but at a rate appropriate to some representative latitude within the field; or to track each latitude independently, using a shearing coordinate system. While developing and validatiing the analysis techniques, we have so far restricted our attention to datasets of no more than a few days in length, so the differential shear over the comparatively small fields of view is not a matter of concern. We have however chosen to use as the base rate for tracking the differential rotation rate suitable to the center of the selected field. This means that the Carrington coordinates describing the field are only applicable at one instant. We describe the field by the Carrington coordinates of its center at the (virtual) time of crossing of the central meridian observed from Earth.

As the data are mapped, they are also apodized in a circularly symmetric pattern, in order to eliminate the effects of non-isotropic higher spatial frequencies in the data resulting from our use of a square field.

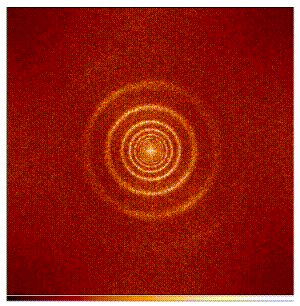
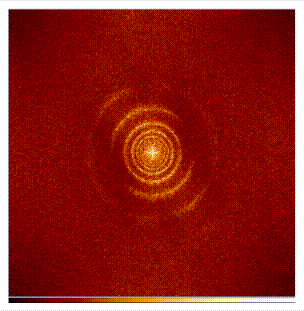
The time series of mapped and apodized data is then Fourier transformed in three dimensions and the three-dimensional k-w power spectrum is computed by standard methods. It is the ease and speed of this calculation that provides the impetus for plane-wave analysis. The eigenmodes organize the power spectrum into surfaces of local peak power of the approximate form w ~ sqrt (k). Two cuts through a typical power spectrum are shown in Fig. 1. The first is equivalent to the plane ky = 0, corresponding to a standard one-dimensional kw (or lv) diagram. The second is a cut through the space at a particular temporal frequency. The characteristic rings of power representing successive eigenmodes of decreasing vertical order with increasing k have inspired the name ``Ring Diagram Analysis'' to this branch of heliseismology.

Up to this point, with the exception of the choice of mapping and tracking, the analysis is quite standard. The real opportunity for efficiency (and different systematic errors) comes in the parametrization of the distortions of the individual eigenmode surfaces. 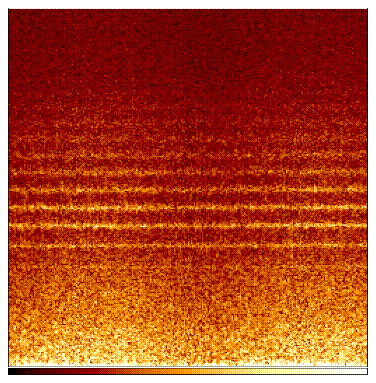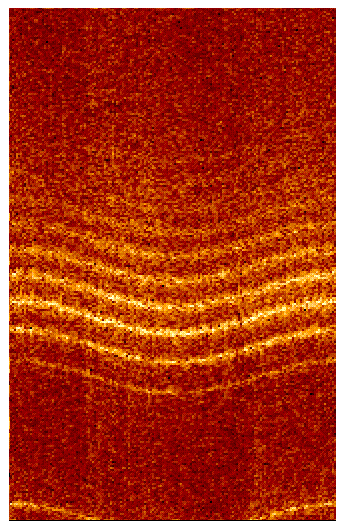Because the first-order effect due to advection is to change the frequency of a given mode by an amount proportional to v·k = vkcos(0), where 0 is the angle between the k vector and the direction of motion, we ``unwrap'' the surface for a given value of k, that is, we make a cylindrical cut through the power spectrum parallel to the w axis, giving P(w,0). The peaks in this two-dimensional power spectrum are a series of nearly straight lines at the eigenfrequencies, with a slight sinusoidal dependence on 0. (See Fig. 2 and Fig. 3). We determine the frequency wn(0) for each eigenmode and then Fourier analyze it. The amplitude and phase of the first order term in the Fourier expansion then give the magnitude and direction, respectively, of the fluid motion. Higher-order terms of course provide information on 2nd-order effects of sound speed variation. This analysis is performed for each clearly identifiable mode and repeated for numerous values of k so that the distortion parameters can be built up as functions of radial order n and horizontal wavenumber k for inversion. Of course the waves are quantized only in the vertical direction by the trapping cavity under our plane-wave assumption, and are continuous in k; the choice of how thick to make the cylindrical cuts and how to space them is arbitrary and essentially dictated by the data resolution. But for spherical-harmonic analysis of oscillations of high spatial frequency in the horizontal direction it is generally impossible to isolate individual eigenmodes by degree and azimuthal order as well.

Discussion

In order to verify and calibrate the present technique we have sought first, to compare the results obtained on a particular data set with those obtained by the original technique independently, and second, to measure the response to known displacements in the data. For this purpose we have used a sample data set from the High-L Helioseismometer at the National Solar Observatory. The data consists of 1024*1024 pixel images taken once per minute in the Ca K line over a period of four observing days from June 22 through June 25, 1993. This dataset is particularly advantageous because it has the same scale and format as the full-disc data we expect in future, and because intensity images are easy to track visually for extended periods, allowing us to verify the tracking involved in data mapping.

We have independently analyzed the same selections from the test dataset using the methods described in Haber et al. (1995) and those described here. We have used and compared independent programs to perform all preliminary stages of the analysis from mapping through determination of the power spectrum, and then have used independent methods of mode identification and parametrization applied to the same power spectra. The actual preliminary results are presented elsewhere (Bogart et al., 1995). Here we focus only on the validation tests.

The primary validation test has been to take a data set consisting of a single day's data (that of June 22, 1993), select a particular region, and then to track the region at each of several different rates in various directions. The tracking rates were not known to those performing the mode parametrizations. 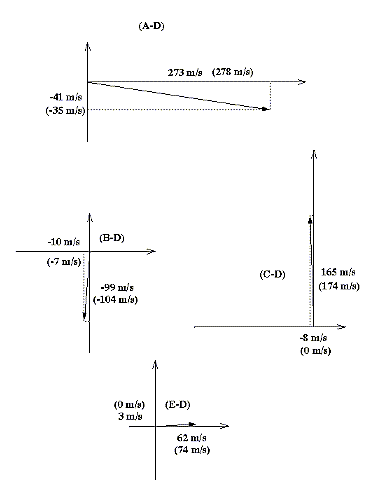Our assumption is that without performing an inversion and without knowing details of the real velocity profile with depth, it must still be true that a uniform translation of the observer will raise or lower the frequencies by a fixed amount for each mode, so that the differences between the inferred vector velocities in two cases for any mode should be the same as the differences in the two artificially generated field velocities. The results from the new method are shown in Figure 5, and those from both methods are given in Table 1. It is clear that both methods generally yield roughly similar results and match the expected velocity differences within about 20 m/s. We consider this a very promising confirmation of the essential power and accuracy of the technique. There are a few noticeable exceptions: The ring diagram technique seriously underestimated the meridional velocity component in one case (C), and both were far from the expected zonal component in case (A). Since this case involved changes in the higher order components in the differential rotation law, this could perhaps expose an error in the tracking program, but we do not have an explanation at this time. More work remains to be done to explore any possible systematic differences between the two methods. It is also of course essential to approach the problem of inversion for the vertical structure of the velocity field as well as 2nd-order effects of sound-speed variations.

Plans for SOI analysis

The Solar Oscillations Investigation (SOI) on SOHO will afford an outstanding opportunity for plane-wave analysis of acoustic modes, with a capability of uninterrupted high-resolution observations continued for full solar rotations and regular daily sampling for extended periods. We plan to conduct the analysis with data processing along the lines outlined here during the Dynamics Program (two months of continuous full-disc observations and one month of continuous high-resolution observations), and during any other time when essentially continuous full-disc and/or high-resolution velocity and/or intensity images are available for a minimum of 3 days.

We will extract maps of each calibrated observable centered on a set of selection points. The mapped subimages for the full-disc field will have an extent of 30 degrees, i.e. extend at least 15 degrees from the selection center in all directions. The mapped regions will be tracked at a constant rotation rate applicable to the latitude of the selection center and referred to the heliographic coordinates of the center at the time of its meridian crossing as observed from Earth. The selection centers from the full-disc data will be located at approximately 15 degree spacings extending as far as ±60 degrees latitude. (The size of the fields will of course be smaller and their spacing correspondingly closer for the high-resolution fields.)

For each time series of tracked regions at a given selection center, we will compute the spatial-temporal power spectra for time samples of about 3 days' (4096 minutes) duration; for a longer data series, multiple power spectra will be computed so that the whole data series is sampled. These power spectra will be analyzed using the procedure described in this note to construct tables of 1st- and probably 2nd-order coefficients in the azimuthal expansion of frequency shifts as functions of radial order and horizontal wave number up to the spatial Nyquist frequency. We believe that the frequency-shift coefficients can be used in that form as the starting point for inversions, but this remains to be established.

References

: Bogart R. S., Sá, L., Haber, D., & Hill, F. 1995. ``Preliminary Results from Plane-Wave Analysis of Helioseismic Data'' 4th SOHO Workshop on Helioseismology, Pacific Grove, California, Apr. 2-6, 1995
: Haber, D., Toomre, J., Hill, F., & Gough D. 1995. ``Local Area Analysis of High-Degree Solar Oscillations: New Ring Fitting Procedures'' 4th SOHO Workshop on Helioseismology, Pacific Grove, California, Apr. 2-6, 1995
: Hill, F. 1988. Ap. J., 333, 996.
: Richardus, P. & Adler, R. K. 1972. Map Projections for Geodecists, Cartographers, and Geographers, North-Holland Publishing Co., Amsterdam.

Tables

Table 1: comparison of inferred velocities and actual velocities in an artificially mistracked region. The method described here is labeled the Fourier method, that described in Haber et al. (1995) the Ring method.
```
Case    Expected       Fourier         Ring
(A)    +352*  -35  | +273   -41  |  +221   -31
(B)      -7  -104  |  -10   -99  |    +1   -81
(C)       0  +174  |   -8  +165  |    +2  +110
(E)     +74     0  |  +62    +3  |   +60    +0
  
* or possibly +278; there may have been an error in the differential rotation
correction involved in this case.
```
Figures
- Figure 1: two standard cuts through the plane-wave power spectrum of a one-day time series of data from the High-L Helioseisomometer. The tracked region is large, extending 30 degrees from its center. The cut shown in (a) is equivalent to a cut along a plane of a particular direction of k; it is actually made by taking azimuthal averages over all values for each k. (b), a ring-diagram, is a cut through a particular temporal frequency w plane, so the two axes are kx and ky.
- Figure 2: A cylindrical cut through the power-spectrum of Figure 1, corresponding to a particular value of k. The vertical axis corresponds to temporal frequency w, the horizontal axis to the azimuthal angle 0 = arctan (ky/kx)
- Figure 3: cylindrical cut through a power-spectrum of High-L Helioseisomometer data deliberately mistracked at a rate equal to twice the solar rotational velocity, i.e. with an apparent east-west motion of 4 km/sec transverse to the line of sight. This enormous artificial velocity enhances the amplitude of the sinusoidal dependence of the ridge locations in azimuth (equivalent to ring displacement) to the point at which it is plainly visible. The phase is appropriate to a nearly pure east-west motion.
- Figure 4: Effect of different mappings. Ring diagrams are shown for the same 4-hour time series of data: (a) using the standard Postel's projection; (b) using a cylindrical equal-area projection. The greater distortion and asymmetry in the rings in case (b) should be evident.
- Figure 5: Average velocity vectors inferred in the test cases using the Fourier method of analysis. For each of the other four test cases, we exhibit the differential velocity relative to the one test case (labeled D) which had no spurious motion; these should be identical to the individual spurious motions, which are given in parentheses. See also Table 1.